An interactive exploration of hexachordal all-combinatoriality in twelve-tone composition
All-Combinatoriality Milton Babbitt, 1987The capacity of a collection to create aggregates with forms of itself and its complement under both transposition and inversion.
Such a collection possesses all four types of combinatoriality: prime-, inversional-, retrograde-, and retrograde-inversional.
3 First-order1 Second-order1 Third-order1 Sixth-orderOnly 6 hexachords in existence are all-combinatorial
What are hexachordally all-combinatorial sets?
A hexachordally all-combinatorial set is a collection of six pitch classes that, when transformed, produces an entirely new set of six pitch classes—its complement.
Interactive Example
The chromatic hexachord H₁ contains C, C#, D, E♭, E, F
Apply T₆ to get H₂: F#, G, G#, A, B♭, B
Combined, they form an aggregate (all 12 pitch classes)!
Key Insight
Hexachordally all-combinatorial sets are extremely rare—only 6 exist out of the 50 possible hexachord types. They form aggregates under all four transformation types, not just some.
The Six All-Combinatorial Hexachords
Each hexachord is shown with its complement. Zeros in the ICV (highlighted in red) indicate missing intervals—the key to combinatoriality.
| Set | H1 (Prime) | H2 (Complement) | ICV | Order | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (A) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | T | E | <543210> | 1stChromatic | |
| (B) | 0 | 2 | 3 | 4 | 5 | 7 | 6 | 8 | 9 | T | E | 1 | <343230> | 1st | |
| (C) | 0 | 2 | 4 | 5 | 7 | 9 | 6 | 8 | T | E | 1 | 3 | <143250> | 1st | |
| (D) | 0 | 1 | 2 | 6 | 7 | 8 | 3 | 4 | 5 | 9 | T | E | <420243> | 2nd | |
| (E) | 0 | 1 | 4 | 5 | 8 | 9 | 2 | 3 | 6 | 7 | T | E | <303630> | 3rdAugmented | |
| (F) | 0 | 2 | 4 | 6 | 8 | T | 1 | 3 | 5 | 7 | 9 | E | <060603> | 6thWhole-tone | |
Understanding the Orders
The "order" indicates how many transposition levels create aggregates. Higher order = more combinatorial flexibility.
First-Order
Sets (A), (B), (C)

First-order sets derive one complement per transformation type. Their ICVs all share the pattern <xxxxx0>—missing only the tritone.
Second-Order
Set (D)

Creates aggregates at two transposition levels. The ICV is missing the minor third (interval class 3).
Under mod12, intervals 3 and 9 are inversions of each other (3 + 9 = 12), hence two transposition levels.
Third-Order
Set (E) — Augmented Scale

Creates aggregates at three transposition levels. Missing both the whole-step and tritone.
Intervals 2 and 10 are inversions (2 + 10 = 12), and 6 maps to itself. This is why it's third-order, not fourth—no fourth-order exists!
Sixth-Order
Set (F) — Whole-Tone Scale

Babbitt called this "the scale for the Frenchman" and "the hexachord he never takes seriously." It's the familiar whole-tone scale.
Missing half-steps, minor thirds, and perfect fourths—three interval classes (and their inversions), hence six transposition levels.
Understanding Interval Class Vectors
Interactive 12-Tone Matrix
This matrix represents Milton Babbitt's second-order hexachord from All Set (1957). Click the buttons to visualize how P₀H₁ forms aggregates with its complements under different transformations.
| I0 | I4 | I5 | I11 | I6 | I10 | I7 | I3 | I1 | I2 | I9 | I8 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P0 | C | E | F | B | F# | Bb | G | Eb | Db | D | A | Ab | R0 |
| P8 | Ab | C | Db | G | D | F# | Eb | B | A | Bb | F | E | R8 |
| P7 | G | B | C | F# | Db | F | D | Bb | Ab | A | E | Eb | R7 |
| P1 | Db | F | F# | C | G | B | Ab | E | D | Eb | Bb | A | R1 |
| P6 | F# | Bb | B | F | C | E | Db | A | G | Ab | Eb | D | R6 |
| P2 | D | F# | G | Db | Ab | C | A | F | Eb | E | B | Bb | R2 |
| P5 | F | A | Bb | E | B | Eb | C | Ab | F# | G | D | Db | R5 |
| P9 | A | Db | D | Ab | Eb | G | E | C | Bb | B | F# | F | R9 |
| P11 | B | Eb | E | Bb | F | A | F# | D | C | Db | Ab | G | R11 |
| P10 | Bb | D | Eb | A | E | Ab | F | Db | B | C | G | F# | R10 |
| P3 | Eb | G | Ab | D | A | Db | Bb | F# | E | F | C | B | R3 |
| P4 | E | Ab | A | Eb | Bb | D | B | G | F | F# | Db | C | R4 |
| RI0 | RI4 | RI5 | RI11 | RI6 | RI10 | RI7 | RI3 | RI1 | RI2 | RI9 | RI8 |
P₀H₁'s Complements
Prime
Inversion
Retrograde-Inversion
Retrograde
Milton Babbitt: All Set (1957)
Intervallic Properties
The second-order hexachord produces what Babbitt calls "a very special kind of twelve-tone double counterpoint."
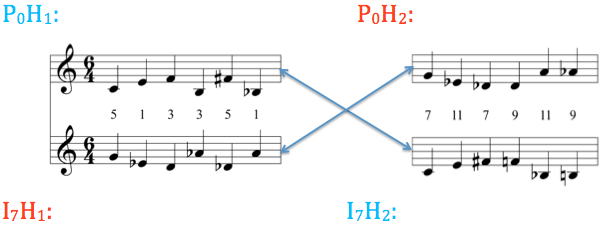
Comparative intervallic content of P₀H₁ and I₇H₂ with their inversionally related complements
Neither set shares an interval—this unique property only occurs with the second-order all-combinatorial set.
"The registrally defined intervals of one hexachord expressing the structurally defined intervals of the other hexachord—a real double counterpoint."
— Milton Babbitt, 1987